View Omega = Sqrt(K/M) UK

omega

View Omega = Sqrt(K/M) UK. It becomes convenient in certain circumstances to just represent sqrt(k/m) as omega because in certain applications (i.e. Sho) it appears all the time, and it has units of angular frequency.

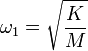
אופני תנודה עצמיים - ויקיפדיה
אופני תנודה עצמיים - ויקיפדיה from upload.wikimedia.org
Perhaps the easiest approach is to consider the following: Then after substitution and simplification. This is easiest if you set x=x_max and v=0 based on the input energy e.

Now, the units of $\omega$ can be obtained directly from (1):

Note that the derivatives of each curve differ in sign. How is the formula for period t = 2pi*sqrt(m/k) derived? Look at a graph of the objects position and over time. # otherwise you will have to include a phase factor to show that you got the exact solution.